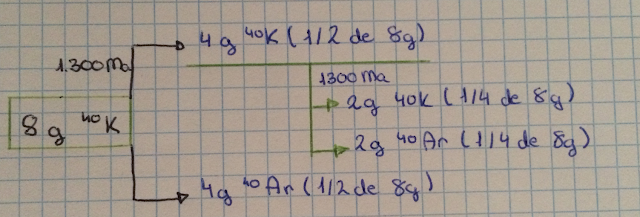Periodo de semidesintegración

En física nuclear y radioquímica se define el período de semidesintegración o constante de semidesintegración, también llamado semivida o hemivida, como el tiempo necesario para que se desintegren la mitad de los núcleos de una muestra inicial de un radioisótopo. Se toma como referencia la mitad de ellos debido al carácter aleatorio de la desintegración nuclear.

El período de semidesintegración no debe confundirse con la vida media. Este concepto es ampliamente utilizado en los cálculos de cinéticas nucleares, para poder caracterizar los nuclidos, como también como un patrón de pureza nuclear de las muestras. Esta constante suele representarse con ${\displaystyle \tau }$.

También se puede entender como el tiempo que tardan en transmutarse la mitad de los átomos radiactivos de una muestra. Un ejemplo es el carbono-14 utilizado para datar restos orgánicos antiguos.

Notación:

• ${\displaystyle t_{1/2}}$ es el período de semidesintegración.
• ${\displaystyle N(t)}$ es el número de núcleos de la muestra en el instante tiempo t.
• ${\displaystyle N_{0}}$ es el número inicial (cuando t = 0) de núcleos de la muestra.
• ${\displaystyle \lambda }$ es la constante de desintegración.

El instante en el que el número de núcleos se ha reducido a la mitad es ${\displaystyle t_{1/2}\,}$. O sea:

${\displaystyle N(t_{1/2})=N_{0}\cdot {\frac {1}{2}}}$

Sustituyendo en la fórmula de decaimiento exponencial:

${\displaystyle N_{0}\cdot {\frac {1}{2}}=N_{0}e^{-\lambda t_{1/2}}\,}$

${\displaystyle e^{-\lambda t_{1/2}}={\frac {1}{2}}\,}$

${\displaystyle -\lambda t_{1/2}=\ln {\frac {1}{2}}=-\ln {2}\,}$

Por tanto, la relación entre el período de semidesintegración de un radioisótopo ( ${\displaystyle t_{1/2}}$ ) y su constante de desintegración ( ${\displaystyle {\lambda }}$ ) es:

${\displaystyle t_{1/2}={\frac {\ln 2}{\lambda }}\,}$

Y como su vida media (${\displaystyle \tau }$) es

${\displaystyle \tau ={\frac {1}{\lambda }}}$

resulta que el período de semidesintegración es aproximadamente el 69,31 % de su vida media.

Si queremos calcular el tiempo que tarda una muestra de un radioisótopo en reducirse al 20 % de la inicial haremos:

${\displaystyle Co}$ = Concentración inicial.

${\displaystyle Ct=0.2*Co}$

${\displaystyle K}$ = Constante de semidesintegración

${\displaystyle t_{1/2}}$ = Periodo de semidesintegración

${\displaystyle t_{1/2}={\frac {\ln({\frac {Co}{Ct}})}{k}}}$

La velocidad de desintegración de un contaminante será menor cuanto menos cantidad de contaminante quede (suponemos que el contaminante sigue una cinética de primer orden).

Periodos de semidesintegración de algunos radionucleidos

Véase también

• Radioisótopo
• Vida media
• Semivida
• Desintegración radiactiva
• Radiactividad